كل ما تُريد معرفته عن الإحصاء الوصفي في البحث العلمي

لكي تطبق الإحصاء الوصفي في البحث العلمي، بشكل محترف، وبدرجة عالية من الكفاءة في التحليل الإحصائي لبحثك العلمي، فأنت بحاجة إلى التعرف على كيفية توظيف البيانات التي قمت بجمعها لتطبيق الإحصاء الوصفي في التحليل الإحصائي للبحث العلمي الخاص بك.

 

 حيث تلعب دورًا كبيرًا في تحديد مسار البحث العلمي؛ لكي يكون بمثابة إضافة علمية مميزة تساعد في سد فجوات مشكلة بحثك محل الدراسة، ومعالجتها بطريقة علمية، وسوف تتعرف معنا على الإحصاء الوصفي وكيفية توظيفه والاستفادة منه في التحليل الإحصائي لبحك العلمي.

 

لأن التحليل الإحصائي من الأساسيات التي تقوم عليها أي رسالة علمية أو بحوث؛ يمكنك قراءة المزيد من المعلومات حول أساسيات التحليل الإحصائي بصورة شاملة؛ من خلال مقالنا.

 

يُعرف  بأنه عدد من الإجراءات الإحصائية التي تصف الخصائص الرئيسية للبيانات محل الدراسة، وتتضمن حزمة معينة من البيانات، ويمكن أن تمثل بيانات الدراسة عينة بحث مثل عينة من السكان أي جزء منهم، أو أن تكون ممثلة للسكان أي عدد السكان بأكملهم.

 

حيث تساعد الإحصائيات الوصفية في توفير ملخصات بسيطة حول العينة والمقاييس ذات الصلة، مثل مقاييس الاتجاه المركزي: مثل الوسط الحسابي، والوسيط، وكذلك مقاييس التشتت مثل التباين، والانحراف المعياري.

 

نلخص لك أهمية الإحصاء الوصفي في البحث العلمي في النقاط الآتية: 

♦تساعد الإحصاء الوصفي في تصور البيانات بطريقة بسيطة، وتقديمها بطريقة هادفة ومفهومة.

♦إنشاء معلومات مفيدة عن طريق ربط المعلومات التي لا معنى لها بشكل فردي؛ لتشكيل معنى مفيد بشكل جماعي.

♦يصف الإحصاء الوصفي في البحث العلمي البيانات المتعلقة بعينة البحث، ويرسم عددًا من الاستنتاجات المتعلقة بالبيانات، حتى لو كانت عينة إحصائية كبيرة، وكذلك النتائج التي يمكن تعميمها على مجتمع العينة.

♦يتم حساب المتوسط ​​الحسابي لدرجات الطلاب كمؤشر على أدائهم العام في موضوع معين؛ حيث لا يمكن تحديد مستوى أداء الطلاب فقط من البيانات الأولية لعلاماتهم.

♦فإن الإحصاءات الوصفية تجعل من الممكن تلخيص، وتقديم مجموعة من البيانات، وخاصة البيانات الكمية المعقدة؛ من خلال مجموعة من الأرقام الجدولية، والرسوم البيانية.

♦على سبيل المثال، إذا أردت حساب المؤشر العام لأداء الطلاب في امتحان نهاية العام لمادة اللغة العربية، فعليك باستخدام مقاييس النزعة المركزية للإحصاء الوصفي؛ فيما يُعرف بالمتوسط الحسابي.

 

للمزيد من المعلومات الوافية حول التحليل الإحصائي للبيانات.

 

تتنوع استخدامات الإحصاء الوصفي في التحليل الإحصائي للبحث العلمي، وسنقوم بعرضها في الآتي:

يتمثل الاستخدام الشائع للإحصاء الوصفي في أنه يتم استخدامه في كل من الدراسات التجريبية والميدانية.

يستخدم الإحصاء الوصفي في حساب جميع المقاييس التي تقوم على وصف طبيعة البيانات التي تم جمعها.

تساعد الإحصاء الوصفي في المساهمة في تقييم نتائج جميع الدراسات البحثية.

 

يتضمن الإحصاء الوصفي عدة أساليب تهدف إلى جمع، وتنظيم، وتلخيص مفردات الدراسة الإحصائية، ثم عرضها بطريقة واضحة، بشكل عام في شكل جداول، أو أشكال رسومية، للسماح بفهم طبيعة العينة محل الدراسة.

يُعد الوصف الجيد، والعرض المناسب لطبيعة البيانات في مقدمة كل دراسة بحثية، أحد الأسس التي يتم على أساسها قياس صحة النتائج مقابل الآخرين، كما يخلق غياب هذه البيانات سؤالًا كبيرًا عند قراءة أو تقييم الدراسة.

تقوم الإحصاء الوصفي على توفير مجموعة واسعة من الوسائل والأساليب التي تساهم بشكل كبير في اكتشاف جميع البيانات الخاصة بالبحث، وتشارك فيها، وهناك نوعان رئيسيان من البيانات وهذان النوعان متمثلان في البيانات الكمية؛ والتي تتمثل في صورة أرقام ورسوم بيانية، والبيانات الكيفية، أو ما تُعرف باسم البيانات النوعية.

تتمثل مقاييس الإحصاء الوصفي في مقياسين أساسيين متمثلين في الآتي:

1.مقاييس النزعة المركزية. 

✦المتوسط الحسابي.

✦الوسيط الحسابي.

✦المنوال.

 

2. مقاييس التشتت، والتي تتضمن الآتي:

✦المدى.

✦التباين.

✦الانحراف المعياري.

 

تابع قراءة موضوع عن أهم برامج التحليل الإحصائي التي يحتاجها الباحثون.

 

أولًا: مقاييس النزعة المركزية Measures of Central Tendency:

توفر مقاييس النزعة المركزية ملخصًا وصفيًّا لمجموعة البيانات، عبر قيمة واحدة تعكس مركز توزيع البيانات، كما لا توفر مقاييس الاتجاه المركزي معلومات حول القيمة الفردية لمجموعة البيانات، ولكنها تهدف بدلًا من ذلك إلى توفير وصف دقيق للبيانات بأكملها في التوزيع، تشمل مقاييس الاتجاه المركزي: المتوسط الحسابي، والوسيط الحسابي، والمنوال، وسيتم شرح كل منهما تفصيليًا في الآتي: 

 

• الوسط الحسابي

يُعرف المتوسط Mean بالوسط الحسابي Arithmetic Mean، ويمكن حسابه؛ من خلال حساب مجموع القيم في مجموعة البيانات، وقسمته على عددها، ويتأثر المتوسط بالقيم المتطرفة؛ وبالتالي فإن أفضل استخدام للوسط الحسابي يكون في التوزيعات المتماثلةsymmetric distributions.

ويتم حساب الوسط الحسابي؛ من خلال المعادلة الاحصائية الآتية: 

الوسط الحسابي= مجموع القيم /عددها.

 

 

• الوسيط الحسابي

الوسيط Median هو القيمة التي تكون في منتصف مجموعة البيانات، ويتم إيجاده عن طريق ترتيب مجموعة البيانات بترتيب تصاعدي أو تنازلي.

فإذا كان عدد البيانات فرديًّا، فتمثل القيمة المتوسطة بها الوسيط الحسابي، أما إذا كان عدد قيم مجموعة البيانات زوجيًّا، فيمكن العثور على القيمة المتوسطة لمجموعة من البيانات بأخذ متوسط القيمتين في المنتصف.

ويتم حساب الوسيط الحسابي من خلال المعادلة التالي:

الوسيط (لمجوعة بيانات عددها زوجي)= مجموع القيمتين في المنتصف / 2.

 

• المنوال (Mode)
•  

هو القيمة الشائعة، أو الأكثر تكرارًا بين البيانات أو المشاهدات.

 

دليل المعرفة لكل ما يتعلق بـ العينات في البحث العلمي.

 

العلاقة بين الوسط، والوسيط، والمنوال

بعد أن قمنا بطرح كل عنصر منهم على حدة نوضح لك أهم فرق بينهم:

المنوال: يكون أكثر فائدة عند استخدامه مع البيانات الاسمية (Nominal Data).

الوسيط: يكون أكثر فائدة عند استخدامه مع البيانات الرتبية (Ordinal Data).

الوسط الحسابي: يكون أكثر فائدة عند استخدامه مع البيانات النسبية، وبيانات الفترة (Interval Data and Ratio Data).

☝ لاحظ أن كل مقياس من مقاييس النزعة المركزية يكون أكثر فعالية مع أنواع معينة من البيانات.

 

 

مثال على مقاييس النزعة المركزية

لكي تتمكن من تطبيق المقاييس التي قمنا بطرحها أعلاه نوضح لك مثالًا عمليًّا، وتطبيقًا لشرح كيفية حساب مقاييس النزعة المركزية في الإحصاءات الوصفية.

• مثال على الوسط الحسابي والوسط

•  
• إذا كان لديك مجموعة البيانات التالية التي تمثل نتائج مادة الرياضيات ل12 طلاب: {10، 5، 9، 8، 6، 5، 9، 8، 7، 6، 5، 6}، فكيف يمكن حساب كل من الوسط الحسابي، والوسيط، والمنوال؟

 

عليك باتباع الخطوات الآتية:

• لحساب الوسط الحسابي عليك بتطبيق قانون الوسط الحسابي؛ وهو مجموع البيانات/عددها= 84/12=7.
•  
•  

حساب الوسيط الحسابي

• عليك أولًا بترتيب البيانات تصاعديًّا: (10-9-9-8-8-7-6-6-6-5-5-5)، ونظرًا؛ لأن عدد قيم البيانات زوجي، يكون الوسيط هو ناتج متوسط العددين في المنتصف: 6 7 / 2 = 6.5.

 

• حساب المنوال

• عليك باستخراج القيمة الأكثر تكرارًا فيها؛ وهما القيمتان (5،6)، ويكون المنوال في هذه الحالة منوالًا ثنائيًّا.
• 
   

ثانياً مقاييس التشتت Measures of Dispersion

 تُعتبر مقاييس الاتجاه المركزي ليست كافية لوصف البيانات؛ حيث يمكن أن يكون لمجموعتين من البيانات نفس المتوسط، ​​ولكن يمكن أن تكون مختلفة تمامًا، وهذا هو السبب في أن مقاييس التشتت تساعد في تفسير تباين البيانات، أي مقدار البيانات المتجانسة، أو غير متجانسة؛ وذلك بفضل المزيد من مقاييس التشتت الأكثر استخدامًا؛ والتي تتمثل في المدى، والتباين، والانحراف المعياري، وسيتم عرضهم تفصيليًّا في الآتي:

 

1.المدى - Range

 يمثل المدى الفرق بين أكبر، وأصغر قيمة في بياناتك، وعلى الرغم من سهولة حسابه إلا أنه يتأثر بدرجة كبيرة بالقيم المتطرفة، ولا يقوم على استخدام جميع القيم في البيانات، ويتم حسابة؛ من خلال المعادلة التالية: 

المدى= أكبر قيمة – أقل قيمة.

 

2. التباين  - Variance

• يمثل التباين Variance متوسط مربع الفرق بين قيم مجموعة البيانات عن الوسط الحسابي، وهو مربع قيم الانحراف المعياري، إلى جانب استخدام هذا المقياس في قياس درجة الانتشار في مجموعة البيانات محل الدراسة، وتتمثل في معادلة حسابها في الآتي:

التباين= مجموع مربع الفرق بين القيم والمتوسط / (عدد القيم -1).

 

 

3. الانحراف المعياري

•  يمثل الانحراف المعياري أكثر مقاييس التشتت استخدامًا، وهو مقياس لمقدار البيانات المنتشرة حول المتوسط​​؛ وهو يساوي الجذر التربيعي لمجموع الانحراف التربيعي عن المتوسط ​​مقسومًا على عدد القيم في مجموعة البيانات مطروح منها، وتتمثل معادلتها في الآتي:

الانحراف المعياري= ((مجموع(القيمة – المتوسط الحسابي)^2/عدد القيم-1))

مثال على مقاييس التشتت

إذا كنت تريد حساب المدى في مجموعة البيانات التالية: {2,4,5,9,8}، فعليك بطرح أكبر قيمة في مجموعة البيانات من أصغر قيمة، 9-2= 7.

إذا كنت تريد حساب الانحراف المعياري في مجموعة البيانات التالية: {4، 2، 5، 6،8}، فعليك أولًا إيجاد المتوسط الحسابي، ومن ثم تقوم بحساب مجموع مربع ناتج طرح كل قيمة من قيم البيانات من المتوسط الحسابي، ثم عليك بإيجاد قسمة المجموع على (عدد القيم- 1)، ثم بأخذ الجذر التربيعي للقيمة ينتج الانحراف المعياري:

المتوسط الحسابي = (4 2 5 6 8) / 5 = 5 (4 - 5) ^2 (2 - 5) ^2 (5 - 5) ^2، (6 - 5) ^2 (8 - 5) ^2 = 20 الانحراف المعياري = (20 /4) √ = 2.236.

• إذا كنت تريد حساب التباين في مجموعة البيانات التالية: {46,69,32,60,52,41}، فعليك بإيجاد المتوسط الحسابي أولًا، ومن ثم إيجاد مجموع مربع ناتج طرح كل قيمة من قيم البيانات من المتوسط الحسابي، ثم تقوم بإيجاد قسمة المجموع على (عدد القيم - 1)؛ ليصبح الناتج يساوي قيمة التباين:

 

المتوسط الحسابي= (46 69 32 60 52 41) / 6 = 50 (46 - 50) ^2 (69 - 50) ^2 (32 - 50) ^2، (60 - 50) ^2 (52 - 50) ^2 (41 - 50) ^2 = 886 التباين = (886 /5) = 177.2.

 

قام فريق العمل في سندك بتجهيز كتاب حول طرق تنفيذ التحليل الإحصائي pdf يوضح لك قوانين الإحصاء الوصفي، وكل ما ترغب في التعرف عليه بصورة شاملة.

 

بإمكانك أن تحصل على نسخة مجانية حول كتاب الإحصاء الوصفيpdf  لكي تستفيد بالمزيد من المعلومات القيمة الموجودة بداخله والاعتماد عليها في تطبيق دراستك، وإذا كان لديك أي مشكلة حول تنفيذ الإحصاءات الوصفية يمكنك طلب الخدمة من شركة سندك نوفر عليك الوقت والجهد. ونطرح أدناه صورة توضح لك مثالًا على تطبيق الإحصاء الوصفي في الأبحاث العلمية.

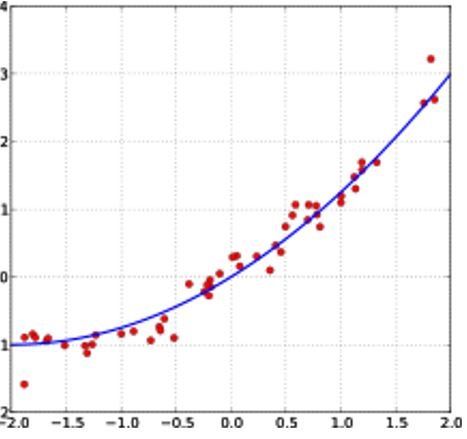
مثال يشرح لك كيفية ظهور النتيجة باستخدام الاحصاء الوصفي

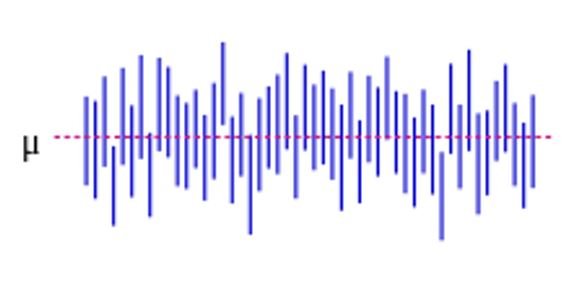
توضح لك هذه الصورة طريقة الإحصاء الوصفي في تمثيل البيانات

 

مراجع يمكنك الرجوع إليها

 

•بلقيدوم، بلقاسم. (2017). دروس في التحليل الإحصائي المعلوماتي باسخدام برنامج Spss.‏

•القطحاني، سعد بن سعيد (2015). الإحصاء التطبيقي: المفاهيم الأساسية وأدوات التحليل الإحصائي الاكثر استخداما في الدراسات والبحوث الاجتماعية باستخدام SPSS. مصر: مركز البحوث والدراسات معهد الإدارة العامة.

 

 

لأنه على الباحث أن يحصل على نتائج دقيقة حول موضوع دراسته فإن الإحصاء الوصفي في البحث العلمي  هي الأداة التي تساعدك في تحقيق ذلك؛ ولذلك قد عرضنا عليك كيفية حساب الإحصاء الوصفي يدويًّا، وتعرفت على أساليب الإحصاء الوصفي، وللمزيد من المعلومات والمعرفة العملية حول Descriptive Statistics.

 

لأننا الأفضل على الإطلاق، جرب بنفسك خدمة التحليل الإحصائي مع موقع إعداد بحوث علمية في شركة سندك؛ لتتمتع بتجربة لا مثيل لها، عبر التواصل الفوري عبر الواتساب للحصول على المزيد من التفاصيل وطلب الخدمة.